 |
생각하는 프로그래밍 -  존 벤틀리 지음, 윤성준 외 옮김/인사이트 |
1996년이라고 기억되는데요.
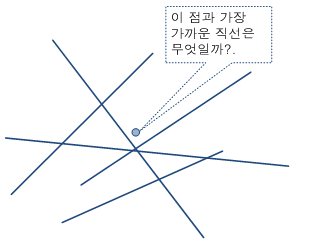
당시 병역특례로 모 증권사의 차트 프로그램을 개발 중이었는데 아래에 있는 그림과 같은 문제 때문에 며칠을 고민한 적이 있었습니다.
위 그림에서처럼 여러 직선이 놓여져 있을 때 사용자가 특정 지점에 마우스를 클릭하면, 클릭한 점과 가장 가까이 있는 직선을 구하는 문제였습니다.
일반적으로 그래픽 프로그램에서 이런 경우가 많은데, 클릭된 곳이 어느 직선 위에 있는 지 또는 허공에 클릭한 것인지 구해야 하는 문제였습니다.
요 문제를 해결하려면, 점과 직선들 사이의 거리를 구한다음 그 중 가장 가까운 거리에 있는 직선을 찾으면 되는, 지금 생각하면, 참 간단한 문제네요.
하지만 당시에는 수학적 지식(중학교 수준 수학인데도!)도 짧고, 망망대해에 떠 있는 직선과 점 사이의 거리를 구하는 게 며칠을 고민하게 만들 정도로 안 풀리는 문제였습니다.
고민만 하고 해결이 되지 않아 우울하던 어느 날, 여느 날처럼 꾸뻑꾸뻑 졸면서 버스를 타고 출근하는데 꿈인지 생시인지 허공에 직선과 점이 나타나서 둘 사이에 직각이 되는 선을 하나 긋는 그림이 생각났습니다.
아하! (이 책의 주제가 되는 단어)
하나의 점과, 직선과의 최단 거리는 점에서 시작해서 직선에 직각이 되는 선을 하나 그어 만나는 두 점 사이의 거리라는 생각이 문득 들었습니다.
그렇다면, 직선에 직각이 되는 선을 하나 그으면 되고, 직각이 되는 선은 이미 알고 있는 직선과 기울기와의 곱이 -1 이 되는 라인이라는 생각까지 미쳤습니다.
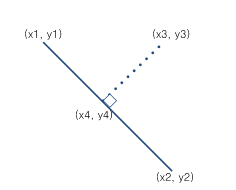
기존 직선의 기울기 A = (Y2 – Y1) / (X2 – X1)
y = Ax + b
에서
(x1, y1) 을 각각 대입해서 b를 구할 수 있었습니다.
이제 남은 건 (x3, y3) 를 지나고 기울기는 직선과 직각이 되는, 즉 –(1/A) 인 직선을 구해야 하는데
y = A’(x – x3) + y3
이고
A’ = -1/A 니까.
y = -1/A(x – x3) + y3
두 직선이 교차하는 점 (x4, y4) 는 아래 두 식에 대입해서 구하면 됩니다.
y = Ax + b
y = -1/A(x – x3) + y3
x4 = (x3 + y3a – ba) / (1 + a2)
y4 = (ax3) + b
그런 다음 (x3, y3) ~ (x4, y4) 의 거리를 구하는 식으로 구하게 되었습니다.
별것도 아닌데 공연히 설명이 길었습니다 ^^;
요기까지 적고 있는데, 수학과를 졸업한 저희 와이프가 낄낄하고 웃더니, 왜 그렇게 어렵게 구하냐고, 직선과 점 사이의 거리를 간단한 공식이 있는데 왜 삽질하냐고 한마디 하는군요 ㅠ_ㅠ;
아니나 다를까 네이버에서 직선과 점 사이의 거리라고 검색하면 무수히 많은 아래와 같은 답변을 쉽게 구할 수 있습니다.
(x3, y3) 에서 직선 ax+by+c=0 까지의 거리 d 는
![]()
명세코, 그 당시에는 네이버라는 훌륭한(정말 훌륭합니다. 흑) 지식검색이 없었습니다. 게다가 똑똑한 와이프도 없었고요.
프로그램을 하다 보면 위와 같이 “아하!” 하고 잘 떠오르지 않은 명쾌한 답변이 갑자기 떠오르는 경우가 많습니다.
이 책 “생각하는 프로그래밍” 은 이처럼 쉽지(?) 않은 문제에 봉착했을 때 “아하!” 하고 명쾌한 답변을 구할 수 있도록 알고리즘 구현에 대한 생각거리를 제시하고 있습니다.
책 이름으로만 본다면 이 책은 네이밍 센스가 아주 좋았던 거 같습니다.
만약 이 책의 원서 제목인 “Programming Pearls 2/E”를 그대로 사용했다면 저 같은 사람은 일단 Pearl 에 대한 책인 줄 알고 구입을 망설였을 것입니다.
그리고 이 책의 주제와 연관된 “알고리즘 극복하기”나 “10일만에 끝내는 알고리즘” 과 같은 식의 제목이었대도 아마 사지 않았을 겁니다.
생각만 해도 머리 아픈 알고리즘 책을 돈 주고 사 볼 용기가 나지 않았을 테니까요.
블로그 계에서 검색엔진 최적화를 위해 제목을 수십 번 심사 숙고해서 짓는 것과 같이 “생각하는 프로그래밍” 이라는 멋진 책 이름이 구입해서 보고 싶게 만든 주 원인 중에 하나였습니다.
책의 전반적인 내용은 전산 학부 시절에 자료구조 같은 과목으로 한번씩 구현해 봤거나 적어도 이름은 들어 본 내용들이 주를 이루고 있습니다.
학교 교재로나 쓰일만한 이러한 내용을 책으로 편 저의(?)가 무엇일까요?
역자 서문에 이런 내용이 나옵니다.
알고리즘과 데이터 구조는 물론 그 자체로도 중요하겠지만, 더욱 중요한 것은 프로그래머로 하여금 문제에 접근하는 방법과 그 문제를 어떻게 해결할지에 대한 방향을 제시한다는데 있다고 할 수 있다
사실 이 책에서 전달하고자 하는 내용은 책에서 구구절절 심도 깊게 파 들어가고 머리 아프게 최적화 하는 코드 그 자체가 아니라, 유한 된 리소스를 어떻게 하면 최대한 활용해서 최고의 성능을 가져올 지 늘 고민하는 프로그래머가 되라는 점입니다.
생각하는 프로그래머가 되기 위해 각 장에서는 훈련을 위한 어려운 질문들이 놓여 있고, 저 같은 허접한 프로그래머가 생각의 과정 없이 자동 반작용으로 선택하게 되는 알고리즘의 문제점을 짚어주고, 조금만 더 깊게 생각하면 메모리를 1/10 만 사용하면서, 속도는 수십, 수백 배가 빨라지는 멋진 알고리즘을 만들 수 있음을 보여줍니다.
책이 워낙 구석기 시대에 나와서 그런지 책에 있는 문제들은 사실 현실과 맞지 않는 부분이 꽤 많습니다.
지금처럼 개인 사용자 PC 의 메모리가 이미 2기가를 넘는 경우도 많은 현실에서, 수 MB 의 메모리는 예전과 같이 용서받지 못할 정도로 문제가 되지 않기 때문에, 이 책의 예제에 조금 공감이 안가는 부분도 많습니다.
게다가 책에서 소개하는 새로운 검색 기법이나 복잡한 알고리즘들은 실제 코딩으로 했을 때 그 복잡성으로 인해 훗날 유지 보수하는 이가 이해할 수 없다고 전혀 손을 댈 수 없거나, 없어질 지도 모르는 문제도 있어 보였습니다. (책에서도 물론, 이러한 알고리즘을 사용할 때 프로파일링을 통해 꼭 필요한 경우인지 여부를 먼저 확인하라고 친절히 설명되어 있긴 합니다만)
책을 읽으면서 제가 그 동안 얼마나 STL 의 편리함에 푹 파묻혀 살았는지 깨닫게 되었습니다.
책에서 질문을 읽자 마자 머리 속에 그려지는 해답은 대부분 STL 에서 제공하는 기본 Container를 사용해서 제 나름대로의 해결책을 생각했었거든요. 물론 저자의 답을 보면, STL 을 사용할때보다 훨씬 나은 성능을 보여주는 코드를 만나게 되어 곧잘 좌절하게 됩니다만, 저같이 업무용 프로그램을 만드는 사람이라면 STL 정도로도 일반적인 문제를 해결하는데 별 어려움이 없어 보였습니다.
대학졸업하고 처음으로 이진 검색과 QSort 의 소스를 본 것 같습니다. ^^;
오랜만에 보니 예전 기억이 떠오르면서 반갑기도 하고, 여전히 쉽지 않은 알고리즘이라는 생각이 들더군요.
이 책에 나오는 내용이 모든 프로그래머에서 큰 도움이 되지는 않겠지만, 누구나 할 수 있는 일반적인 해결책보다, 예술가에 가까운 멋지고, 아하! 소리 나는 생각하는 프로그래머가 되고 싶은 분들이면 도서관에서 연필 붙잡고 이 책을 읽어 보세요 :-)
그리고 이 책을 읽다 보니 어딘가에서 본 아래 문구가 계속 떠오르더군요. 구글 뉴스 그룹에선가 답변을 다는 친구가 늘 답변의 끝에 붙이는 내용인데, 혹시 정확한 의미를 해석해 주실 분 계신가요?
영어가 짧아 마지막 and wrong 을 어떤 식으로 받아 들여야 할지 난감하더군요. 앞 구절(모든 복잡한 문제에는 간단하고 멋진 해결책이 있다는)만 보면 참 멋진 말 같은데 and wrong 때문에 뭐가 뭔지 잘 모르겠습니다
“For every complex problem, there is a solution that is simple, neat, and wrong.”
H. L. Menkin
'나의 서재' 카테고리의 다른 글
| [책]소프트웨어, 누가 이렇게 개떡같이 만든 거야 (3) | 2008.06.10 |
|---|---|
| [책]Code Craft 짧은 서평 (8) | 2008.03.09 |
| [책]Programming Ruby(프로그래밍 루비) (10) | 2008.02.03 |
| [책]뉴욕의 프로그래머 (12) | 2007.12.31 |
| [책] Ship it! 성공적인 소프트웨어 개발 프로젝트를 위한 실용 가이드 (2) | 2007.10.22 |
| [책]실용주의 프로그래머 (2) | 2007.10.05 |
댓글